Fields-Medaillen in Mathematik, die von vier unter 40-Jährigen gewonnen wurden

Die meisten großen Mathematiker haben dieses Thema schon in jungen Jahren entdeckt und sich oft bei internationalen Wettbewerben hervorgetan.

Mathematik hingegen war ein Schwachpunkt der in Kalifornien geborenen und in Südkorea aufgewachsenen June Huh. „Ich war in den meisten Fächern gut, außer in Mathe“, sagte er. „Die Mathematik war im Durchschnitt bemerkenswert mittelmäßig, was bedeutet, dass ich bei einigen Tests ziemlich gut abgeschnitten habe, bei anderen aber fast durchgefallen bin.“

Als Teenager wollte Dr. Huh Dichter werden, und er verbrachte zwei Jahre nach der High School damit, dieser kreativen Beschäftigung nachzugehen. Aber keine seiner Schriften wurde jemals veröffentlicht. Als er die Seoul National University besuchte, studierte er Physik und Astronomie und erwog eine Karriere als Wissenschaftsjournalist.

Rückblickend erkennt er mathematische Einsichten aufblitzen. In der Mittelschule spielte er in den 90er Jahren ein Computerspiel, „The 11th Hour“. Das Spiel enthielt ein Puzzle aus vier Rittern, zwei davon schwarz und zwei weiß, die auf einem seltsam kleinen Schachbrett platziert waren.

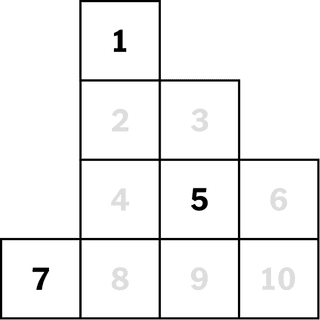
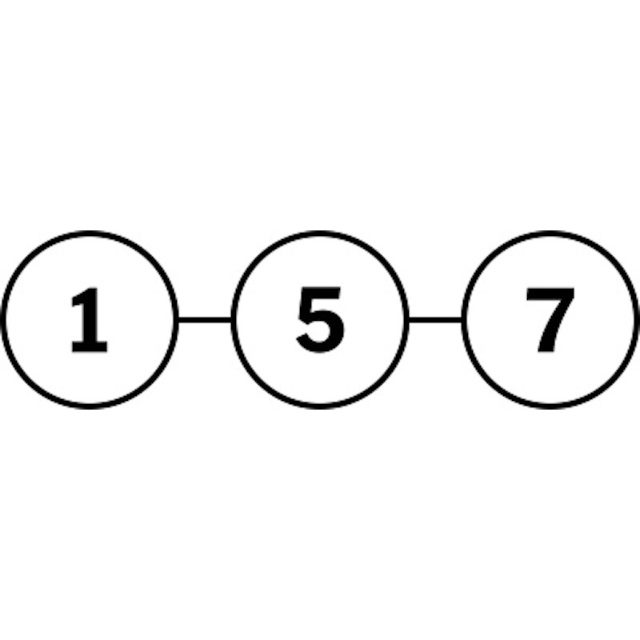
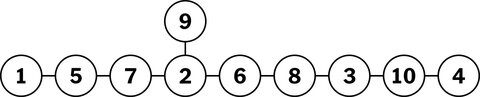
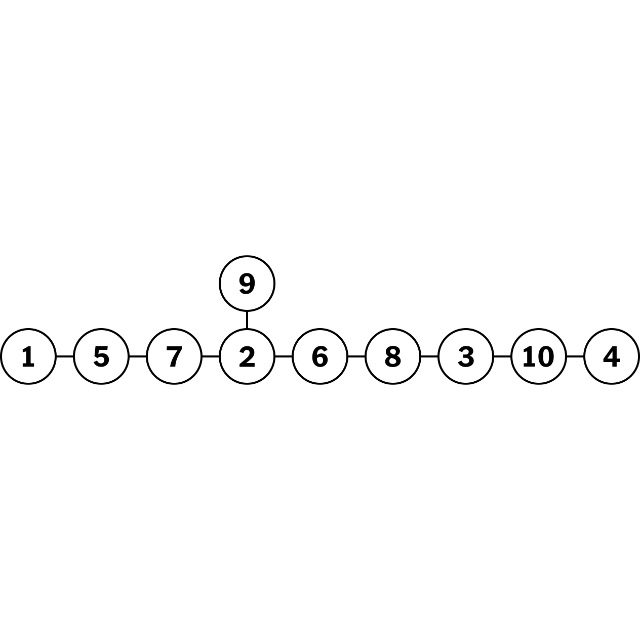
Die Aufgabe bestand darin, die Positionen der schwarzen und weißen Ritter zu tauschen. Er verbrachte mehr als eine Woche damit, umzufallen, bevor ihm klar wurde, dass der Schlüssel darin bestand, die Felder zu finden, auf die sich die Ritter bewegen konnten. Das Schachpuzzle kann als Diagramm umformuliert werden, bei dem jeder Springer auf ein benachbartes unbesetztes Feld ziehen kann und die Lösung leichter zu erkennen ist.

Die Neuformulierung mathematischer Probleme durch Vereinfachung und Übersetzung in einer Weise, die die Lösung klarer macht, war der Schlüssel zu vielen Durchbrüchen. „Die beiden Formeln sind logisch nicht zu unterscheiden, aber unsere Intuition funktioniert nur in einer von ihnen“, sagte Dr. Huh.

Siehe auch  „Squid-Game-Wahlen“: Südkoreas Wahlkampf wird hässlich

Mathematisches Denkrätsel

Mathematisches Denkrätsel

hier drüben Puzzle schlug Jun huh:

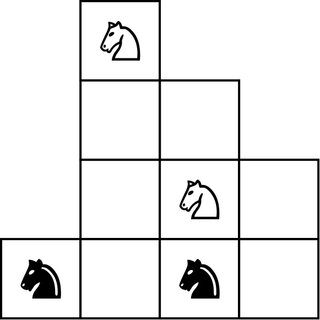
Tor: Die schwarzen und weißen Ritter tauschen ihre Positionen. →

Mathematisches Denkrätsel

Viele Spieler stolpern auf der Suche nach einem Muster durch Versuch und Irrtum. Das hat Dr. Huo getan, und Er hätte aufgeben können Nach Hunderten von Versuchen.

Dann erkannte er, dass das einfach geformte Brett und die Bewegungen der L-förmigen Springer irrelevant waren. Entscheidend sind die Beziehungen zwischen den Quadraten.

ein Problem umschreiben in Etwas leichter zu verstehen Es ist oft ein Schlüssel für Mathematiker, um Durchbrüche zu erzielen.

Mathematisches Denkrätsel

Wir luden ein Quadratische Nummerierung damit wir es verfolgen können.

Mathematisches Denkrätsel

Ich empfehle Springer auf Feld 1. Er kann nur auf Feld 5 ziehen, während der Springer mit der Nummer 5 auf 1 oder 7 ziehen kann.

Mathematisches Denkrätsel

Das könnte sein als Netzplan dargestellt Was Mathematiker einen Graphen nennen. Die Linien zeigen an, dass der Fahrer zwischen den Feldern 1 und 5 und zwischen den Feldern 5 und 7 radeln kann.

Mathematisches Denkrätsel

Erweitern Sie diese Analyse um ein einzelnes geformtes Schachbrett Dieses Diagramm wird erstellt:

Jetzt können wir die Jockeys in dieses Diagramm eintragen, die weißen Jockeys auf die Felder 1 und 5 und die schwarzen Jockeys auf die Felder 7 und 9.

Mathematisches Denkrätsel

Das Problem ist nach wie vor der Positionstausch zwischen schwarzen und weißen Rittern. Für jede Bewegung kann der Fahrer in einen benachbarten leeren Knoten gleiten.

Die überarbeitete Version ist Viel einfacher herauszufinden. Hier ist eine Antwort:

Mathematisches Denkrätsel

Verwenden Sie die Grafik mit Nummerierte Knoten als Kieferringdann finden wir die Bewegungen auf dem Originalbrett.

Mathematisches Denkrätsel

Präsentieren des gleichen Puzzles auf diese neue Weise, die das Wesentliche des Problems besser enthüllt, Plötzlich war die Lösung klarsagte Dr. Huo. „Es hat mich dazu gebracht, darüber nachzudenken, was es bedeutet, etwas zu verstehen.“

Siehe auch  „Ich bin bereit für Verhandlungen“ mit Putin, aber wenn sie scheitern, könnte das „Dritter Weltkrieg“ bedeuten

Die Mathematik entdeckte er erst in seinem letzten Studienjahr wieder, als er 23 Jahre alt war. In diesem Jahr war Hisuki Hironaka, der japanische Mathematiker, der 1970 die Fields-Medaille gewann, Gastprofessor an der Seoul National University.

Dr. Hironaka unterrichtete einen Kurs über algebraische Geometrie, und Dr. Huh nahm daran teil, lange bevor er seinen Doktortitel erhielt, weil er dachte, er könnte einen Aufsatz über Dr. Hironaka schreiben. „Er ist in den meisten Teilen Ostasiens wie ein Star“, sagte Dr. Huh über Dr. Hironaka.

Dr. Huh sagte, dass der Kurs anfänglich mehr als 100 Studenten angezogen habe. Aber bald fanden die meisten Schüler den Stoff unverständlich und brachen den Unterricht ab. Dr. Huo fuhr fort.

„Nach etwa drei Vorlesungen waren wir zu fünft“, sagte er.

Dr. Huo fing an, mit Dr. Hironaka zu Mittag zu essen, um über Mathematik zu diskutieren.

„Er sprach meistens mit mir“, sagte Dr. Huh, „und mein Ziel war es, so zu tun, als würde ich etwas verstehen und richtig antworten, damit das Gespräch weitergeht. Es war eine schwierige Aufgabe, weil ich es nicht wirklich wusste was ist passiert.“

Dr. Huh machte seinen Abschluss und begann mit Dr. Hironaka an seinem Master-Abschluss zu arbeiten. Als Dr. Huh sich 2009 an etwa einem Dutzend Top-Schulen in den Vereinigten Staaten für seinen Ph.D.

„Ich war ziemlich zuversichtlich, dass ich trotz all der gescheiterten Mathematikkurse in meinem Bachelor-Zeugnis einen begeisterten Brief von einem Fields-Medaillengewinner erhalten hatte, sodass ich von vielen Graduiertenschulen angenommen werden würde.“

Alle bis auf einen lehnten ihn ab – die University of Illinois Urbana-Champaign setzte ihn auf eine Warteliste, bevor sie ihn schließlich akzeptierte.

„Es waren ein paar sehr interessante Wochen“, sagte Dr. Huh.

In Illinois begann er mit Arbeiten, die ihn auf dem Gebiet der Kombinationen nach vorne brachten, dem Gebiet der Mathematik, das die Anzahl der Möglichkeiten quantifiziert, auf die Dinge gemischt werden können. Auf den ersten Blick sieht es aus, als würde man mit Tinker Toys spielen.

Stellen Sie sich ein Dreieck vor, ein einfaches geometrisches Objekt – was Mathematiker einen Graphen nennen – mit drei Kanten und drei Scheitelpunkten, wo sich die Kanten treffen.

Man kann dann damit beginnen, Fragen zu stellen, wie z. B. bei einer bestimmten Anzahl von Farben, wie viele Möglichkeiten es gibt, die Scheitelpunkte einzufärben, da keiner von ihnen die gleiche Farbe haben kann? Der mathematische Ausdruck, der die Antwort gibt, wird als chromatisches Polynom bezeichnet.

Komplexere chromatische Polynome können für komplexere geometrische Objekte geschrieben werden.

Unter Verwendung von Werkzeugen aus seiner Arbeit mit Dr. Hironaka bewies Dr. Ho Reeds Vermutung, die die mathematischen Eigenschaften dieser chromatischen Grenzmodifikatoren beschrieb.

Im Jahr 2015 demonstrierte Dr. Huh zusammen mit Eric Katz von der Ohio State University und Karim Adepracito von der Hebrew University of Jerusalem Rotas Theorie, die abstraktere kombinatorische Objekte, die als Matroids bekannt sind, anstelle von Dreiecken und anderen Graphen beinhaltete.

Für Matroide gibt es eine weitere Gruppe von Polynomen, die ein ähnliches Verhalten wie chromatische Polynome zeigen.

Ihr Beweis wurde in ein mystisches Stück algebraischer Geometrie gezogen, das als Theorem von Hodge bekannt ist und nach William Vallance Douglas Hodge, einem britischen Mathematiker, benannt ist.

Aber was Hodge entwickelte, „war nur ein Beispiel für diese mysteriöse und universelle Manifestation des gleichen Musters in allen mathematischen Disziplinen“, sagte Dr. Huh. „Die Wahrheit ist, dass wir, selbst die Top-Experten auf diesem Gebiet, nicht wirklich wissen, was es ist.“